GeoWerkstatt-Projekt des Monats April 2024
Projekt: Integrity and Collaboration in Dynamic Sensor Networks (i.c.sens)
Forschende: Qianqian Zou
Projektidee: The research project is focused on ensuring the trustworthiness of autonomous systems, such as self-driving cars and service robots, to prevent them from posing threats to humans. This involves investigating how to effectively utilize the signals from various sensors within these systems to enhance their safety and reliability.
In autonomous systems, uncertainty-aware localization is a crucial component for navigating complex and dynamic environments. Due to sensor noise, measurement errors, and environmental variability, there is inherent uncertainty in the measurements, reference maps and the models used for localization. A thorough investigation of uncertainty-aware localization can enhance the precision of localization results and yield dependable measures of uncertainty, thereby mitigating the possibility of navigation errors.
One common approach for uncertainty-aware localization is to use probabilistic methods. There are many probabilistic localization approaches available that can help achieve robust localization by accounting for measurement outliers. However, most of these approaches do not take into account the impact of reference map errors on localization accuracy.
This study investigates the effects of uncertain maps on localization performance. The study advocates for the adoption of the Markov Chain Monte Carlo (MCMC) technique as a more efficient alternative to the traditional MC approach. The MCMC method is predicated on the principle of generating particles through a Markov chain, which enables a more directed exploration of the state space, thereby reducing the number of particles needed to achieve a comparable level of accuracy.
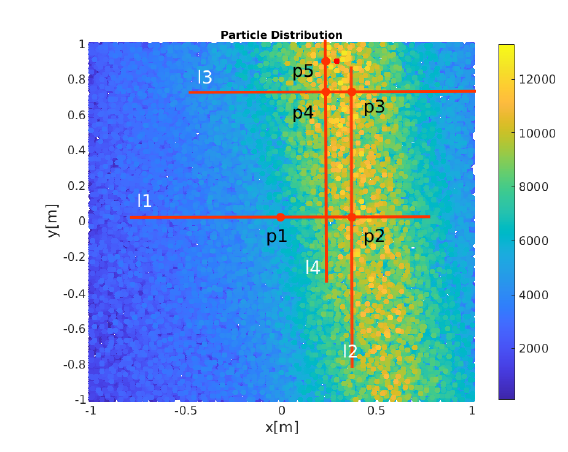
The following figure illustrates an example of the MCMC process. We see each transformation as a particle and the initial particle commences at position p1. At each step, the next state is selected based on a probability distribution conditioned on the current state. Through successive iterations, this particle transitions across the state space, e.g., from p1 move to p2, p3, p4, ultimately arriving at position p5. This p5 transformation will be selected to correct the initial position.

 ©
ikg
©
ikg
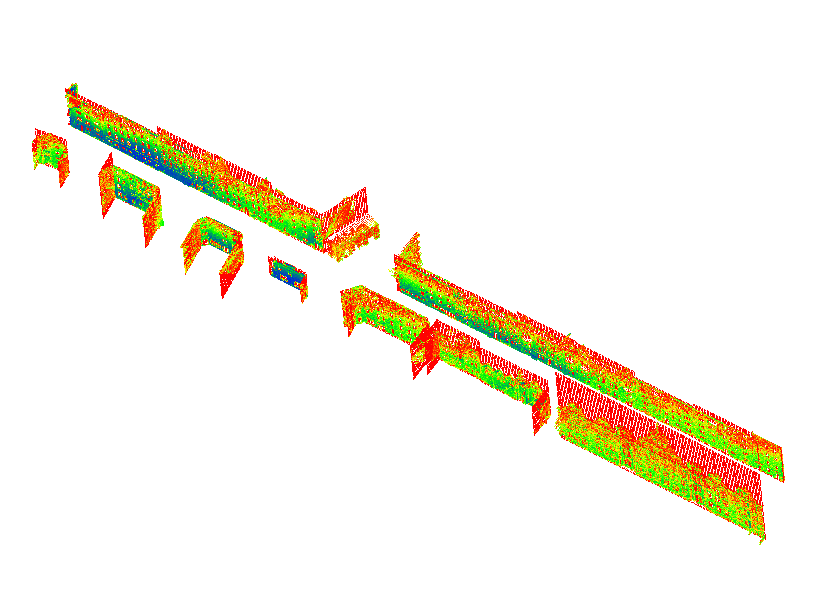
In the conducted experiments, an uncertain map is utilized as the reference framework. The uncertain map provides the depth of the surface for each coordinate, with associate standard deviation along the surface normal. The noisy Velodyne scan points are matched with the reference map to correct the pose. In MCMC-based localization techniques, the reference map is systematically converted into a probabilistic occupancy map. The noisy scan points with the wrong initial pose will be transformed and fall into probabilistic occupancy cells. Based on the overall count for the occupancy probability of all points, a score function can be optimized and a best transformation can be found to correct the point clouds, so that the points will align better with the reference map. The corresponding sensor position can be accordingly corrected by the same transformation matrix. The following figures present an example of the uncertain map and the scan data.
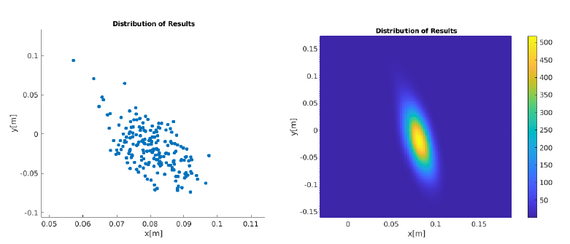
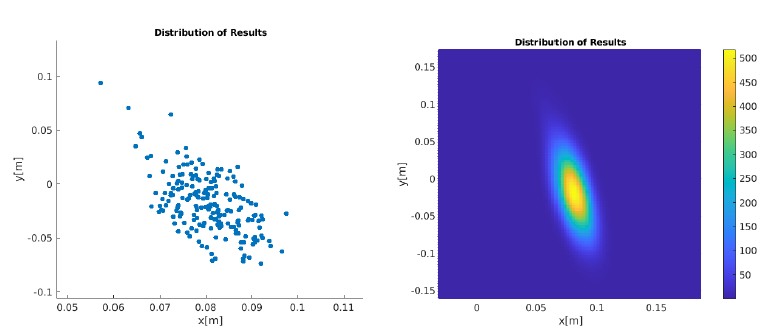
Additionally, to understand how uncertain maps affects localization results, the study generates multiple maps that are sampled from the map distribution. This group of maps are then utilized in localization, providing a set of localization results (blue points in the figure). From these points, we can see a pattern, and thus, the localization distribution (right on the figure) is derived. This approach enables a quantitative analysis of how uncertainties within the map influence the precision and reliability of localization. An investigation into the uncertainty propagation through the localization process will be further studied in future.
 ©
ikg
©
ikg