Pro Punkt eine Punktewolke

Projekt: Pro Punkt eine Punktewolke

Forschende: Dominik Ernst

Projektidee: Pro Punkt eine Punktewolke: Wie man Zufallszahlen zur Unsicherheitsanalyse verwenden kann.

Autonome Fahrzeuge sind ein wichtiger Baustein der Mobilitätswende. Die Skepsis ist jedoch noch hoch - häufig hört man Aussagen wie „Ich würde mich nicht trauen, mich in so ein selbstfahrendes Auto zu setzen.“ Wie vertrauenswürdig sind diese Fahrzeuge tatsächlich?  

Einer der wichtigsten Faktoren ist, wie die Fahrzeuge ihre Umgebung über verschiedene Sensoren wahrnehmen. Treten dabei Probleme auf, beeinflussen sie alle weiteren Schritte, denn es gilt „Garbage in, garbage out.“ Sprich: Statt „Datenmüll“ sind hochpräzise Sensordaten nötig, damit sich ein autonomes Fahrzeug auf Basis verlässlicher Informationen sicher durch die Straßen bewegt. 

Häufig stammen die Daten von Laserscannern, auch LiDAR (light detection and ranging) genannt. LiDAR senden aktiv Infrarotlaserstrahlen aus und tasten damit die Umgebung mit bis zu einer Million Punkte pro Sekunde ab. Diese Punkte ergeben ein Bild der Umgebung, eine Punktwolke, aus der die eigene Position lokalisiert oder Hindernisse erkannt werden.

Wie präzise nimmt das LiDAR die einzelnen Punkte der Punktwolke auf? Diese Frage untersuchen wir in diesem Projekt mit einer Unsicherheitsanalyse. Die Punktwolken werden dabei von einem auf einem Roboter montiertem LiDAR aufgezeichnet (Abbildung1).

Der Mess-Aufbau

Es gibt vielfältige Einflüsse, die eine Messung verfälschen können. Um die Anzahl der Faktoren zunächst möglichst gering zu halten, haben wir die Untersuchungen im 3D-Labor des Geodätisches Instituts durchgeführt. Hier sind einige Einflüsse konstant, etwa die Temperatur oder die Luftfeuchtigkeit, und andere Einflüsse sind nicht vorhanden, etwa direkter Sonnenschein. Die zu beachtenden Einflussfaktoren bei der Messung sind der Sensor an sich, die zu messenden Objekte, die Konstellation zwischen Sensor und Objekt, sowie die Kombination der Sensoren im System.

Während der Sensor für die Messung feststeht und damit nicht geändert werden kann, ist die Wahl der Objekte, die gemessen werden, sehr wichtig. Der ausgesandte Laserstrahl interagiert mit dem Objekt: Dunkle Oberflächen oder flache Auftreffwinkel sorgen für ungenauere Messungen, da der reflektierte Laserstrahl schwächer bzw. „zerstreuter“ zurückkommt. Wir verwenden weiß beschichtete Aluminiumplatten, da diese eine ideale Oberfläche für das Scanning darstellen. In einem geschlossenen Raum sind zudem die maximalen Distanzen, die der Laserstrahl zurücklegt, beschränkt. Das reduziert ebenfalls mögliche Abweichungen.

Wenn man mit mehreren Sensoren arbeitet, brauchen alle aufgenommenen Daten einen „Zeitstempel“. Damit stellt man sicher, dass die Daten zur gleichen Zeit und damit – bei einem sich bewegenden System – auch am gleichen Ort aufgenommen wurden. Die Zeitstempel müssen sich auf die gleiche Uhr beziehen. Schon kleine Verzögerungen (Millisekunden) zwischen den internen Uhren der Sensoren können zu großen Abweichungen führen, wenn die Sensordaten fusioniert werden. Außerdem müssen die Daten räumlich „zueinanderpassen“. Ähnlich wie Fotos, die man zueinander zuordnet, um ein großes Bild zusammenzufügen, müssen auch zwischen den Daten der verschiedenen Sensoren die entsprechenden Verschiebungen (Wie überlappen die Daten?) und Rotationen (Sind die Daten zueinander verdreht?) bestimmt werden. In 3D kommt man für diese so genannte Transformation auf drei Verschiebungen (Translationen) und drei Rotationen.

Die Messungen

Die Messungen staffeln sich in zwei Etappen: Zunächst ermitteln wir bei der Kalibrierung die Transformationsparameter zwischen den verschiedenen Sensoren. Neben den eigentlichen Parametern werden auch die Unsicherheiten dieser Werte ermittelt, welche später noch wichtig werden. Im nächsten Schritt bewegt sich der Roboter durch den Raum und nimmt die Punktwolken auf. Der Laser Tracker beobachtet die T-Probe, welche eine direkte Beobachtung der räumlichen Transformation ermöglicht. Die T-Probe verfügt dabei nicht nur über einen Reflektor sondern auch über LEDs, die zur Berechnung der Orientierung verwendet werden können. Die Transformation ist notwendig, um die Punktwolken mit den weißen Referenzplatten im Raum vergleichen zu können.

Die Bewertung der Ergebnisse erfolgt ebenfalls in zwei Schritten. Im ersten Schritt wird die Punktwolke in den Raum transformiert und mit den Referenzplatten verglichen. Damit kann die Distanz von den Punktwolken zu den Platten berechnet werden. In einer perfekten Welt wären die Distanzen Null, da aber keine Messung perfekt ist, ergeben sich Abweichungen. Diese Abweichungen entstehen bei den Messungen des LiDARs, aber auch bei der Kalibrierung und der Messung der Bewegung. Damit liegt die mittlere Abweichung der Punktwolke im Vergleich zu Referenzumgebung bei 10,0 mm.

Die Berechnung der Unsicherheiten

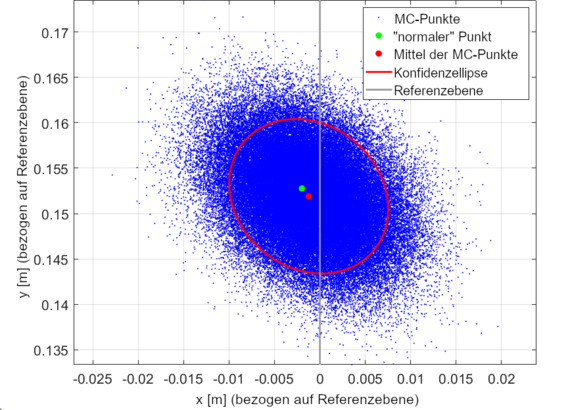
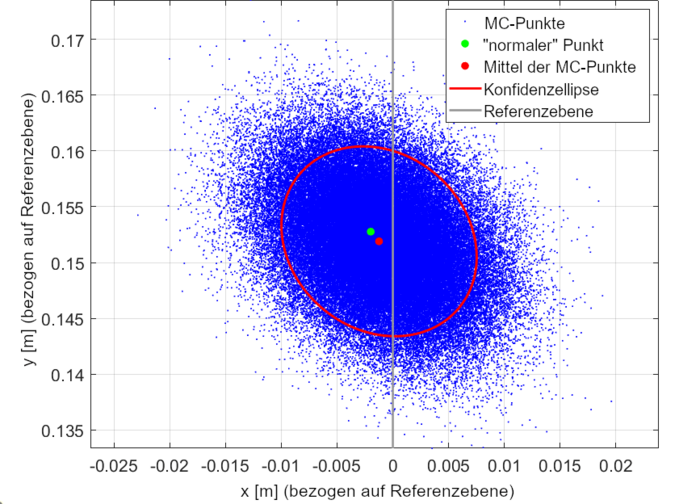
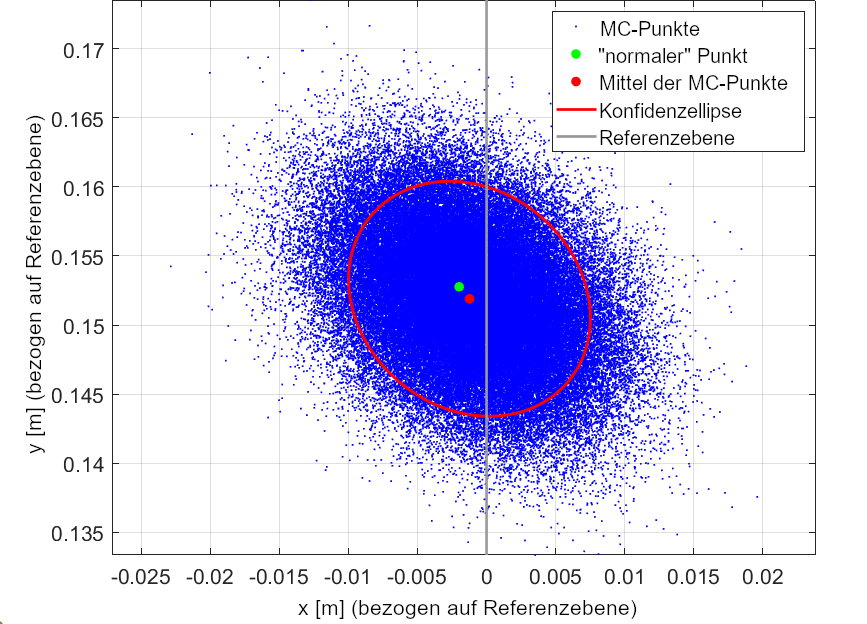
Nun kommt der zweite und für dieses Projekt entscheidende Schritt: die Berechnung der Unsicherheiten der Punkte. Dazu wird auf Monte Carlo (MC) Methoden zurückgegriffen. Der Name leitet sich aus den Kasinos in Monaco ab, da bei MC-Methoden Zufallszahlen verwendet werden. Die Basis, auf der diese Zufallszahlen erzeugt werden, ist entscheidend für die Aussagekraft der Ergebnisse. Und hier kommen die zuvor berechneten Unsicherheiten ins Spiel. Während der Kalibrierung werden die Unsicherheiten der Messelemente des LiDARs mitgeschätzt und nun genutzt, um für jeden Punkt der Punktwolke eine eigene Punktwolke zu generieren. Für jeden gemessenen Punkt werden so 100.000 MC-Punkte mit zufallsgenerierten Abweichungen erzeugt. Je größer die Abweichungen, desto größer die Unsicherheiten des Punktes. Die Punktwolken der Punkte werden anschließend auch in den Raum transformiert, wobei jeweils die Unsicherheiten der Zwischenschritte ebenfalls mittels Zufallszahlen integriert werden. Am Ende können die MC-Punkte für jeden Punkt der Punktwolke verwendet werden, um eine Unsicherheit abzuleiten. Die Ergebnisse für einen Punkt aus der Punktwolke sind in Abbildung 2 gezeigt. Dabei zeigt sich, dass die Berechnung der Punktpositionen über die MC-Punkte zu kleineren Abweichungen führen, sodass die mittlere Abweichung auf 8.1 mm sinkt. Außerdem zeigt sich, dass die Abweichungen im Rahmen der vorhergesagten Unsicherheiten liegen.

Um die hier vorgestellte Unsicherheitsmodellierung weiterzuentwickeln, werden wir weitere Einflussfaktoren hinzunehmen. Etwa Faktoren, die für Anwendungen im Außenbereich notwendig sind. Zudem sollte die Methode auch für andere Systeme nutzbar werden. Auch die Berechnungsmethode ist zu hinterfragen: Während die MC-Methode flexibel in der Anwendung ist, ist sie durch die zusätzlichen Punkte sehr rechenintensiv, sodass ein Einsatz in Echtzeitsystemen unmöglich ist.